
前言
前段时间看到有大佬对.net 6.0新出的PriorityQueue(优先级队列)数据结构做了解析,但是没有源码分析,所以本着探究源码的心态,看了看并分享出来。它不像普通队列先进先出(FIFO),而是根据优先级出队。
ps:读者多注意代码的注释。
D叉树的认识(d-ary heap)
首先我们在表示一个堆(大顶堆或小顶堆)的时候,实际上是通过一个一维数组来维护一个二叉树(d=2,d表示每个父节点最多有几个子节点),首先看下图的二叉树,数字代表索引:
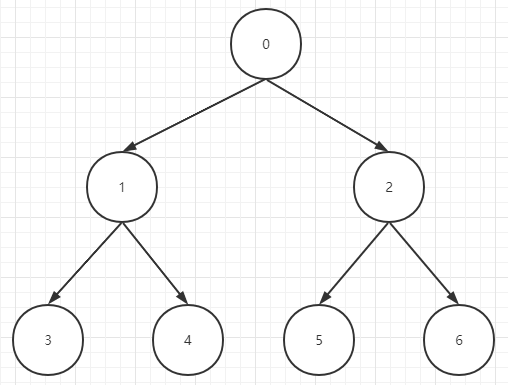
1、任意一个节点的父节点的索引为:(index - 1) / d
2、任意一个节点的左子节点的索引为:(index * d) + 1
3、任意一个节点的右子节点的索引为:(index * d) + 2
4、它的时间复杂度为O(logndn)
通过以上公式,我们就可以轻松通过一个数组来表达一个堆,只需保证能拿到正确的索引即可进行快速的插入和删除。
源码解析
一、构造初始化
关于这部分主要介绍关键的字段和方法,比较器的初始化以及堆的初始化,请看如下代码:
public class PriorityQueue<TElement, TPriority>
{
/// <summary>
/// 保存所有节点的一维数组且每一项是个元组
/// </summary>
private (TElement Element, TPriority Priority)[] _nodes;
/// <summary>
/// 优先级比较器,这里用的泛型,比较器可以自己实现
/// </summary>
private readonly IComparer<TPriority>? _comparer;
/// <summary>
/// 当前堆的大小
/// </summary>
private int _size;
/// <summary>
/// 版本号
/// </summary>
private int _version;
/// <summary>
/// 代表父节点最多有4个子节点,也就是d=4(d=4时好像效率最高)
/// </summary>
private const int Arity = 4;
/// <summary>
/// 使用位运算符,表示左移2或右移2(效率更高),即相当于除以4,
/// </summary>
private const int Log2Arity = 2;
/// <summary>
/// 构造函数初始化堆和比较器
/// </summary>
public PriorityQueue()
{
_nodes = Array.Empty<(TElement, TPriority)>();
_comparer = InitializeComparer(null);
}
/// <summary>
/// 重载构造函数,来定义比较器否则使用默认的比较器
/// </param>
public PriorityQueue(IComparer<TPriority>? comparer)
{
_nodes = Array.Empty<(TElement, TPriority)>();
_comparer = InitializeComparer(comparer);
}
private static IComparer<TPriority>? InitializeComparer(IComparer<TPriority>? comparer)
{
//如果是值类型,如果是默认比较器则返回null
if (typeof(TPriority).IsValueType)
{
if (comparer == Comparer<TPriority>.Default)
{
return null;
}
return comparer;
}
//否则就使用自定义的比较器
else
{
return comparer ?? Comparer<TPriority>.Default;
}
}
/// <summary>
/// 获取索引的父节点
/// </summary>
private int GetParentIndex(int index) => (index - 1) >> Log2Arity;
/// <summary>
/// 获取索引的左子节点
/// </summary>
private int GetFirstChildIndex(int index) => (index << Log2Arity) + 1;
}单元总结:
1、实际所有元素使用一维数组来维护这个堆。
2、调用方可以自定义比较器,但是类型得一致。 如果没有比较器,则使用默认的比较器。
3、默认一个父节点最多有4个子节点,D=4时效率好像是最好的。
4、获取父节点索引位置和子节点索引位置使用位运算符,效率更高。
二、入队操作
入队操作操作相对简单,主要是做扩容和插入处理,请看如下代码:
public void Enqueue(TElement element, TPriority priority)
{
//拿到最大位置的索引,然后再将数组长度+1
int currentSize = _size++;
_version++;
//如果长度相等,说明已经到达最大位置,数组需要扩容了才能容下更多的元素
if (_nodes.Length == currentSize)
{
//扩容,参数是代表数组最小容量
Grow(currentSize + 1);
}
if (_comparer == null)
{
MoveUpDefaultComparer((element, priority), currentSize);
}
else
{
MoveUpCustomComparer((element, priority), currentSize);
}
}
private void Grow(int minCapacity)
{
//增长倍数
const int GrowFactor = 2;
//每次扩容的最小值
const int MinimumGrow = 4;
//每次扩容都2倍扩容
int newcapacity = GrowFactor * _nodes.Length;
//数组不能大于最大长度
if ((uint)newcapacity > Array.MaxLength) newcapacity = Array.MaxLength;
//使用他们两个的最大值
newcapacity = Math.Max(newcapacity, _nodes.Length + MinimumGrow);
//如果比参数小,则使用参数的最小值
if (newcapacity < minCapacity) newcapacity = minCapacity;
//重新分配内存,设置大小,因为数组的保存在内存中是连续的
Array.Resize(ref _nodes, newcapacity);
}
private void MoveUpDefaultComparer((TElement Element, TPriority Priority) node, int nodeIndex)
{
//nodes保存副本
(TElement Element, TPriority Priority)[] nodes = _nodes;
//这里入队操作是从空闲索引第一个位置开始插入
while (nodeIndex > 0)
{
//找父节点索引位置
int parentIndex = GetParentIndex(nodeIndex);
(TElement Element, TPriority Priority) parent = nodes[parentIndex];
//插入节点和父节点比较,如果小于0(默认比较器情况下构建的小顶堆),则交换位置
if (Comparer<TPriority>.Default.Compare(node.Priority, parent.Priority) < 0)
{
nodes[nodeIndex] = parent;
nodeIndex = parentIndex;
}
//算是性能优化吧,不必检查所有节点,当发现大于时,就直接退出就可以了
else
{
break;
}
}
//将插入节点放到它应该的位置
nodes[nodeIndex] = node;
}单元总结:
1、首先记录当前元素最大的索引位置,根据适当的情况来扩容。
2、扩容正常情况下是以2倍的增长速度扩容。
3、插入数据时,从最后一个节点的父节点向上还是找,比较元素的Priority,交换位置,默认情况下是构建小顶堆。
三、出队操作
出队操作简单来说就是将根元素返回并移除(也就是数组的第一个元素),然后根据比较器将最小或最大的元素放到堆顶,请看如下代码:
public TElement Dequeue()
{
if (_size == 0)
{
throw new InvalidOperationException(SR.InvalidOperation_EmptyQueue);
}
//将堆顶元素返回
TElement element = _nodes[0].Element;
//然后调整堆
RemoveRootNode();
return element;
}
private void RemoveRootNode()
{
//记录最后一个元素的索引位置,并且将堆的大小-1
int lastNodeIndex = --_size;
_version++;
if (lastNodeIndex > 0)
{
//堆的大小已经被减1,所以将最后一个元素作为副本,开始从堆顶重新整理堆
(TElement Element, TPriority Priority) lastNode = _nodes[lastNodeIndex];
if (_comparer == null)
{
MoveDownDefaultComparer(lastNode, 0);
}
else
{
MoveDownCustomComparer(lastNode, 0);
}
}
if (RuntimeHelpers.IsReferenceOrContainsReferences<(TElement, TPriority)>())
{
//将最后一个位置的元素设置为默认值
_nodes[lastNodeIndex] = default;
}
}
private void MoveDownDefaultComparer((TElement Element, TPriority Priority) node, int nodeIndex)
{
(TElement Element, TPriority Priority)[] nodes = _nodes;
//堆的实际大小
int size = _size;
int i;
//当左子节点的索引小于堆的实际大小时
while ((i = GetFirstChildIndex(nodeIndex)) < size)
{
//左子节点元素
(TElement Element, TPriority Priority) minChild = nodes[i];
//当前左子节点的索引
int minChildIndex = i;
//这里即找到所有同一个父节点的相邻子节点,但是要判断是否超出了总的大小
int childIndexUpperBound = Math.Min(i + Arity, size);
//按照索引区间顺序查找,并根据比较器找到最小的子元素位置
while (++i < childIndexUpperBound)
{
(TElement Element, TPriority Priority) nextChild = nodes[i];
if (Comparer<TPriority>.Default.Compare(nextChild.Priority, minChild.Priority) < 0)
{
minChild = nextChild;
minChildIndex = i;
}
}
//如果最后一个节点的元素,比这个最小的元素还小,那么直接放到父节点即可
if (Comparer<TPriority>.Default.Compare(node.Priority, minChild.Priority) <= 0)
{
break;
}
//将最小的子元素赋值给父节点
nodes[nodeIndex] = minChild;
nodeIndex = minChildIndex;
}
//将最后一个节点放到空闲出来的索引位置
nodes[nodeIndex] = node;
}单元总结:
返回根节点元素,然后移除根节点元素,调整堆。
从根节点开始,依次查找对应父节点的所有子节点,放到堆顶,也就是数组索引0的位置,然后如果树还有层数,继续循环查找。
将最后一个元素放到堆适当的位置,然后再将最后一个位置的元素置为默认值。
四、总结
通过源码的解读,除了了解类的设计之外,更对对优先级队列数据结构的实现有了更加深刻和清晰的认识。
 18180749853
18180749853 蜀ICP备2021001672号